ViT and MLP-Mixer
2025-05-02
NLP를 공부하던 중, Vision에 대해 알아보게 된 배경을 짧막하게 한글로 작성하겠습니다!
NLP를 다루던 중 갑자기 ViT인가 싶을텐데요. 실은 이번 주에 가졌던 커피챗에서 ViT와 CNN의 차이가 뭔지에 대한 질문을 받았습니다. 눈 앞에 놓인 목적만을 최대한 잘 완수하기 위해 Vision field를 완전히 배제하다보니 image processing을 모른 채 답변을 했습니다.
처음에는 CNN은 filter size로 제한된 convolution 연산을 하고, ViT는 transformer 구조로 입력값의 관계를 전부 계산한다. 그러므로 context window 크기가 근본적인 차이다. 라고 말했습니다. (물론 이렇게 깔끔하게 이야기하기보다 벙벙 돌려가며 이야기했습니다.)
그러자 2차 질문으로 그렇다면 transformer input context size를 인위적으로 제한해 CNN과 동일하게 만든다면 어떻게 될까요? 다시 말해 context size가 동일한 상황이라면 ViT와 CNN은 무슨 차이일까요? 가 돌아왔습니다. 질문을 주신 분이 느긋하게 화장실까지 다녀오시는 동안 머리가 깨져라 생각했는데요. Convolution 연산 방식이 어떻게 이루어지는지만 알고 있을 뿐, 실제로 응용 이론이나 CNN만의 특징은 모르는 상태였습니다. 그러나 질문자분은 제가 ViT를 모른다는 걸 알고 계시기에 오히려 의도 파악을 하고 transformer의 근본적인 구조를 고민했습니다.
처음에는 당연히 Query, Key, Value라는 attention operation을 떠올렸습니다. convolution operation은 filter의 입력으로 들어온 값들의 relationship을 계산하도록 설계된 게 아니므로 이 차이인가 싶었는데, 실은 동일한 context size에서 deep neural network를 통해 학습하다보면 Transformer만큼은 아니더라도 당연히 filter size 안의 관계성이 parameter들에 담길 것이라 생각했습니다. 그렇다면 어느정도는 Q, K, V를 흉내내는 거나 다름 없으므로 근본적 차이는 아니라 생각했습니다. (실제로 아래 내용에서 후술될 inductive bias 관점에서 locality가 그러한 관계성을 보입니다.) 그러나 Cross-attention이라고 하기엔... 애초에 Encoder, Decoder 구조라는 다른 차원의 이야기를 꺼내오는 거라 이 또한 설득력이 낮다고 생각했습니다.
위와 같은 생각의 흐름을 쭉 전달드리고서 결국 잘 모르겠다.라고 말씀드렸습니다. 그러자 여기에는 정답이 없지만, 그럼에도 근본적인 차이는 Multi-head attention이라 생각한다는 말에 '아차' 싶었습니다. Transformer 구조에서 head의 개수가 늘어날수록 다양한 특징을 학습해 표현력이 높아지고, 또 해석 가능한 AI를 연구하시는 분들도 각각의 Head가 가진 latent representation이 뭔지 탐색한다는 어딘가 박혀있던 기억들이 새록새록 떠올랐습니다. Convolution 연산은 대상이 image든 natural language든 대상이 가진 잠재적 특성을 '다양하게' 고려하지 않습니다. 그저 하나의 값으로 표현할 뿐이죠.
이 물음에 대해서 ViT와 MLP-Mixer를 공부했더라도 답변하지 못했던 건 매 한가지였을 겁니다. 왜냐하면 두 논문에서도 주요하게 다뤄지는 건 Context size와 이로 인해 생기는 inductive bias의 차이니까요. 오히려 context size 관점에서 벗어나지 못해 더 엉뚱한 이야기를 했을지도 모릅니다. 그러나 MLP-Mixer가 가져다주는 통찰도 있습니다. 바로 inductive bias든 multi-head attention이든 두 대상이 잠재적인 특성을 다룬다는 겁니다.
이와 같은 implicit한 의미들을 신경망 구조에서 어떻게 이끌어낼 수 있을까요? 수학적 논리력도 중요하겠지만, 무엇보다도 언어와 인간의 지각 처리 과정에 대한 깊은 이해, 그리고 탁월한 직관력이지 않을까 생각해봅니다. 알면 알수록 참 재미있는 세계인 듯해요!
Before diving into this topic, I'd like to highlight an exceptional YouTube Video that brilliantly illustrates the concepts of image processing and what is 'inductive bias'.
Initially, I'll examine the groundbreaking Vit Paper.

In abstract,
When pre-trained on large amounts of data and transferred to multiple mid-sized or small image recognition benchmarks (ImageNet, CIFAR-100, VTAB, etc.), Vision Transformer (ViT) attains excellent results compared to state-of-the-art convolutional networks while requiring substantially fewer computational resources to train.
A critical factor in this approach is the necessity for training on extensive datasets. Due to the nature of inductive bias, transformer architectures require substantial amounts of data to achieve optimal performance.
Following the transformer's remarkable success in NLP, numerous attempts have been made to adapt this architecture to the image processing domain.
However, these initial efforts yielded disappointing results that fell short of expectations. The researchers of ViT attributed this underperformance to a fundamental architectural difference:
Transformers lack some of the inductive biases inherent to CNNs, such as translation equivariance and locality, and therefore do not generalize well when trained on insufficient amounts of data.
This analysis led to a pivotal breakthrough in their research:
We find that large scale training trumps inductive bias.
So, what does this actually imply? what precisely is 'inductive bias', and why is a substantial volume of data necessary?
Before exploring these questions, let's first understand the ViT architecture.
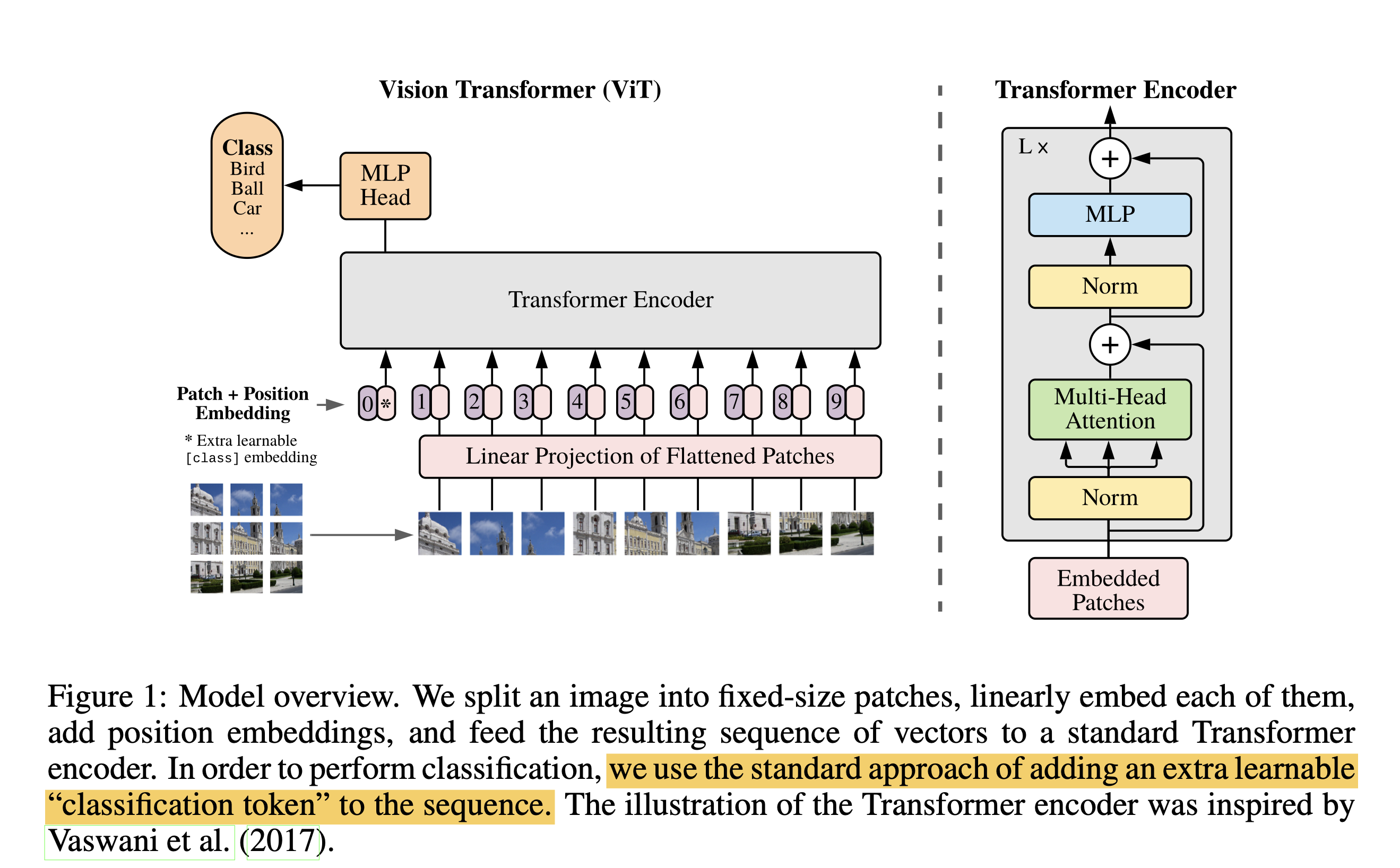
ViT requires the input to be divided into fixed-size segments, known as PxP patches.
The original image dimensions are represented as (H, W, C), corresponding to Height, Width, and Channel respectively. The N patches each have dimensions of (P, P, C), where N = H*W/P^2
After splitting the image into the patches:
The Transformer uses constant latent vector size D through all of its layers, so we flatten the patches and map to Ddimensions with a trainable linear projection (Eq. 1). We refer to the output of this projection as the patch embeddings.
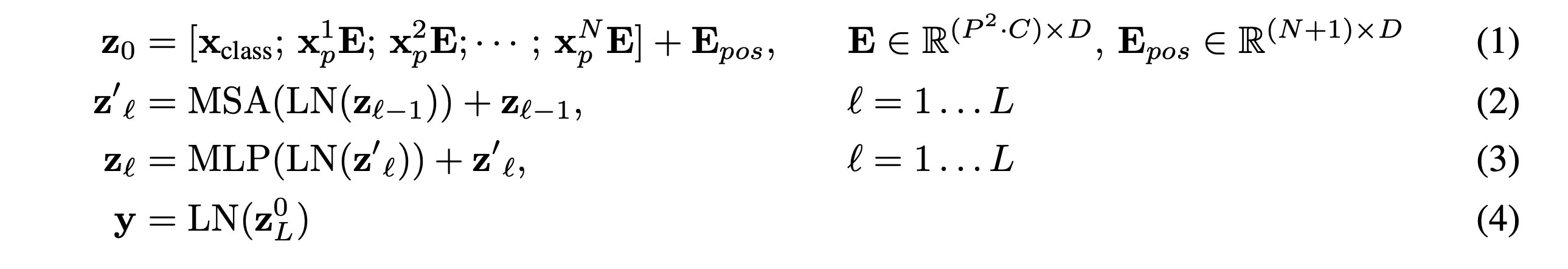
In equation (1), xE represents the embedding vector that serves as input for the self-attention operation. Furthermore, the subsequent equations elucidate the operation performed by the architecture, as illustrated in Figure 1.
For those already familiar with 'self-attention' mechanisms, the fundamental distinction between CNN and ViT becomes evident: context scope. While ViT computes relationships across all patches simultaneously during self-attention, CNNs only process interactions between adjacent patches during convolution. This distinction represents the essence of inductive bias.
Inductive bias refers to the inherent predispositions or assumptions within a model that facilitate generalization, thereby enhancing performance. How does this mechanism function? In machine learning contexts, the objective is to identify a predictor that minimizes loss. Throughout this optimization process, inductive bias serves a vital function in mitigating overfitting. Calibrating an appropriate degree of inductive bias is crucial, as suboptimal values can either lead to overfitting or compromise overall performance.

In CNNs, locality, two-dimensional neighborhood structure, and translation equivariance are baked into each layer throughout the whole model. In ViT, only MLP layers are local and translationally equivariant, while the self-attention layers are global.
The authors explain that CNNs inherently possess locality and translation inductive biases, while ViT lacks these specific predispositions. At this point, this distinction prompts a crucial question: Is transformer completely devoid of inductive bias?
Well, I explained inductive bias as 'predispositions or assumptions within a model'. It means that inductive bias enhance a model's predictive capabilities when confronted with novel scenarios-situations the model hasn't encountered during its training phase. Following this rationale, both CNNs and transformers inherently possess inductive biases, although the former has structural inductive bias, while the latter has global inductive bias.
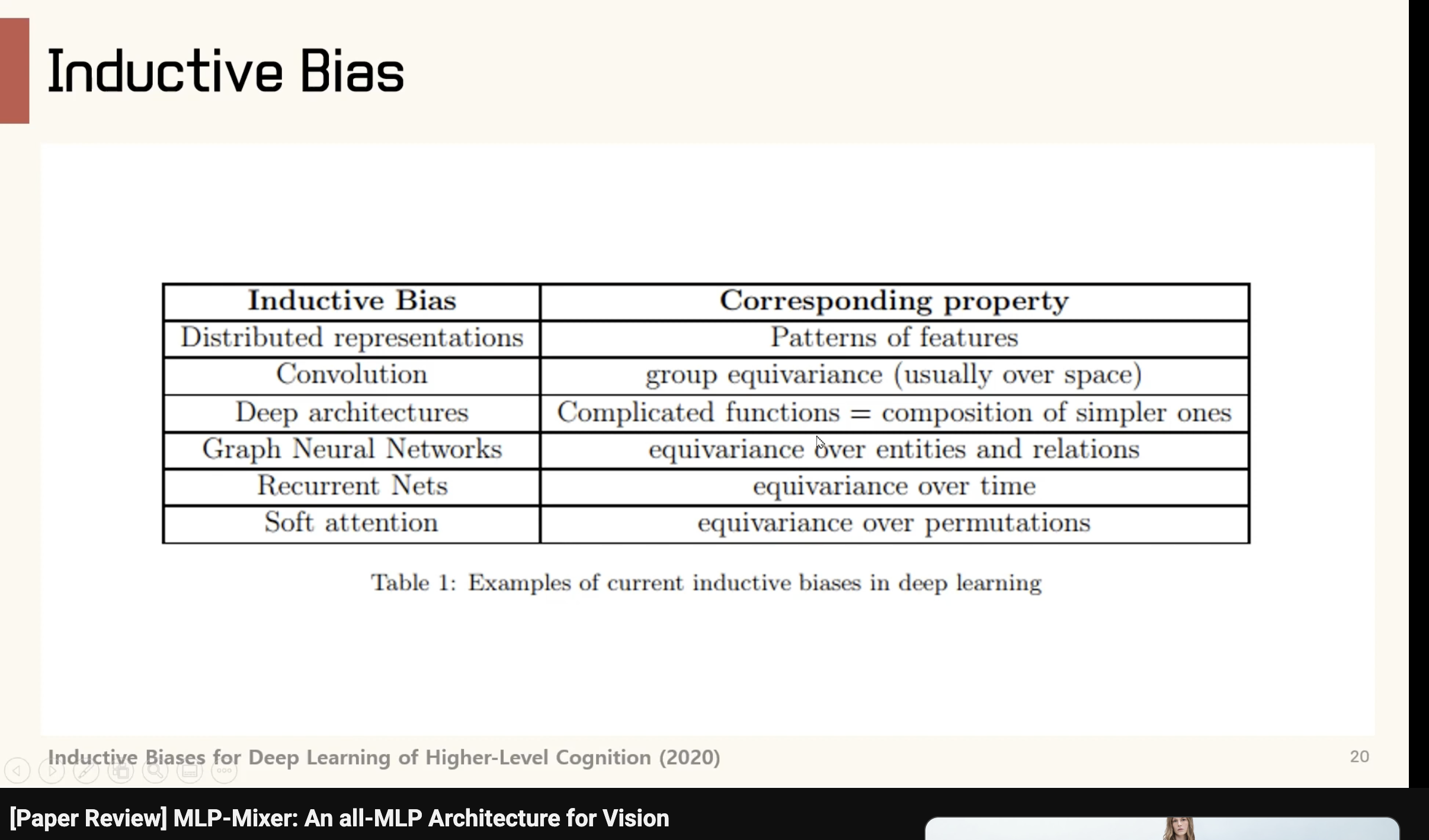
Structural inductive bias can be effectively learned from comparatively smaller datasets than those required for global inductive bias. This distinction is intuitively comprehensible: establishing meaningful correlations across all input elements and identifying appropriate patterns for model generalization presents a substantially more complex challenge.
MLP-Mixer effectively exemplifies this intuition through its linear computational complexity processes: Token-mixing MLP and Channel-mixing MLP.
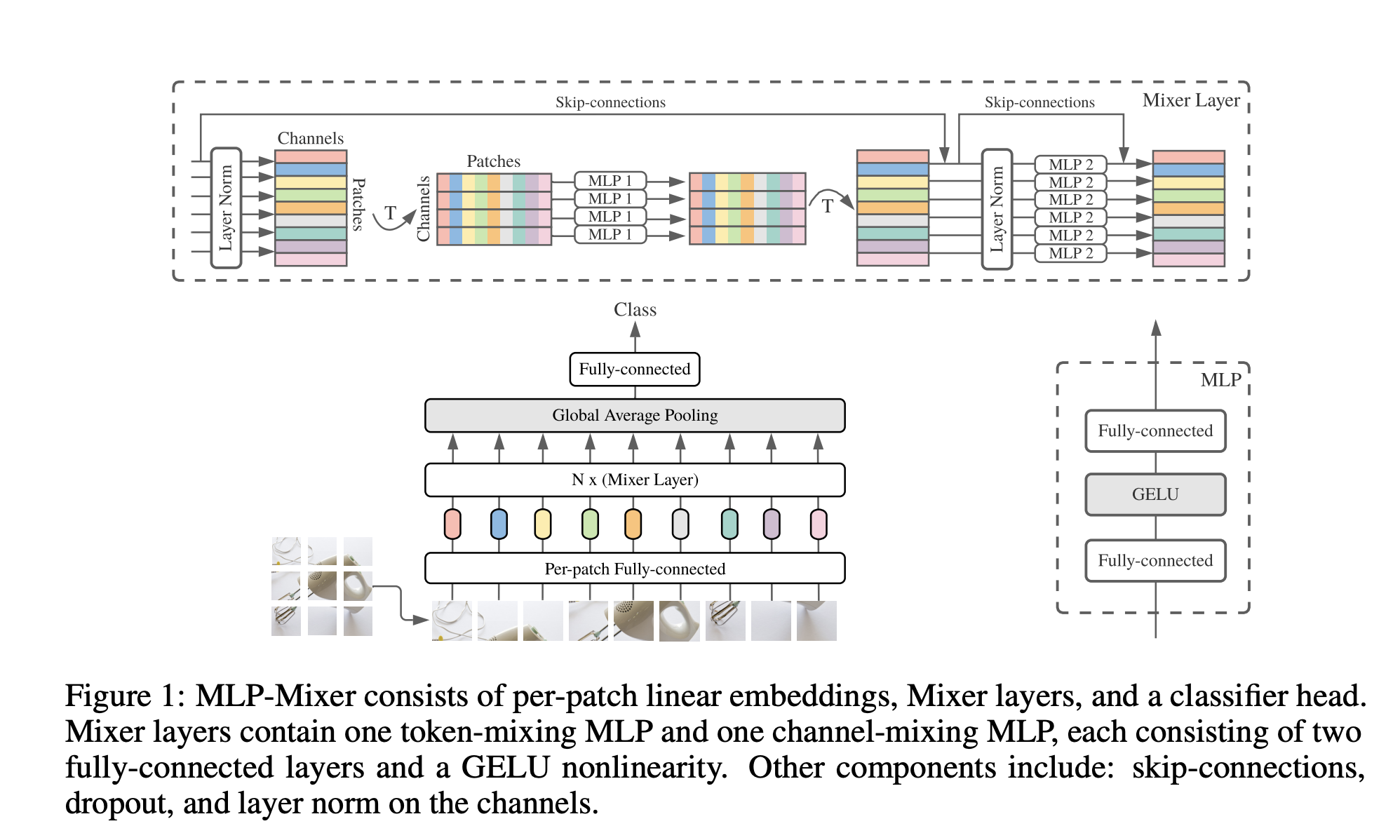
This architecture represents not merely a novel approach that is considerably more streamlined than either ViT or CNNs, but also an evolutionary synthesis derived from both CNNs and transformers. The authors characterize MLP-Mixer as an expanded conceptualization of CNNs.
Through this architectural attempt, the presence of inductive bias becomes evident, enabling us to understand its attributes.
we would like to understand the inductive biases hidden in these various features and eventually their role in generalization
Reference
Paper Review MLP-Mixer: An all-MLP Architecture for Vision - https://www.youtube.com/watch?v=Y-isY31Thkw ViT Paper: https://arxiv.org/pdf/2010.11929.pdf MLP-Mixer Paper: https://arxiv.org/abs/2105.01601